IRROTATIONAL FLOW OF AN INVISCID FLUID
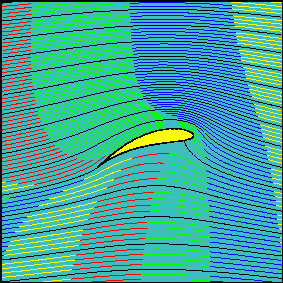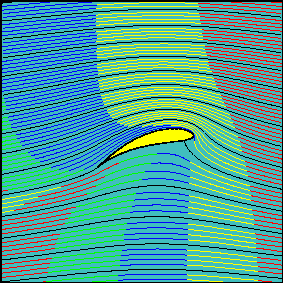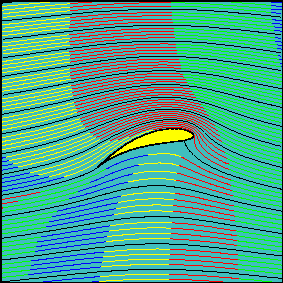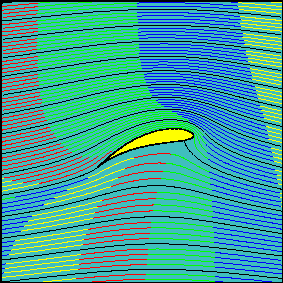

This lecture is devoted to the study of irrotational plane flows of an inviscid fluid. The ultimate goal is to determine the force exerted by a uniform flow on a Joukowski wing (airfoil). It should be noted that, as in a wind tunnel, the force would be the same if the wing moves with the same velocity in a fluid at rest.
In the absence of shear stresses, forces exerted on a body - the wing in this case - by an inviscid fluid are always normal to the surface and due to the pressure. The force on the body is obtained through the determination of the flow and pressure fields on the surface of the object.
It will be shown that this force is always directed at a right angle with respect to flow (lift), that it is proportional to the fluid velocity far from the body and to the circulation around the profile. The component of the force in the direction of the flow (drag) is always zero. This apparent paradox can only be solved by dropping the hypothesis of irrotational (and inviscid) flow in a region close to the body (boundary layer) where viscosity plays a fundamental role and the flow is rotational and viscous.
Nevertheless, boundary layer theory, not to be considered herein, shows that pressure forces are transported throughout the boundary layer without being altered, if separation is absent. Thus, the information obtained on lift by means of the irrotational theory can be regarded as a good approximation of the actual lift of the wing.
A table of contents follows:
 |
Elements of irrotational flow theory Some elementary notions of Fluid Mechanics are recalled to fully understand the solution methodology. |
 |
Examples of elementary irrotational flows Some simple analytic solutions of irrotational plane flows are shown. More complex flows can be created by superposition (linear combination) of these simple solutions. |
 |
Flow around a cylinder The irrotational flow around a cylinder is analyzed in terms of flow and pressure fields. Animations show how the solution is affected by changing the circulation around the cylinder. |
 |
Joukowski transformation The conformal transformation due to Joukowski is able to transform the flow domain around a cylinder into the flow domain around a Joukowski wing profile. An interactive application allows the user to experiment with the parameters of the transformation creating different wing profiles. |
 |
Flow around a wing The irrotational flow around a wing is analyzed in terms of flow and pressure fields. Animations show how the solution is affected by changing the angle of attack of the wing. |
A sequential browsing of the various pages is suggested, at least for first time visitors.
 Back to cover page
Back to cover page